Notes on fastai Book Ch. 13

ai
fastai
notes
pytorch
Chapter 13 provides a deep dive into convolutional neural networks.
Author

Christian Mills

Published

March 29, 2022

This post is part of the following series: 
#hide
# !pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
#hide
from fastai.vision.all import *
from fastbook import *

matplotlib.rc('image', cmap='Greys')
import inspect
def print_source(obj):
    for line in inspect.getsource(obj).split("\n"):
        print(line)

Convolutional Neural Networks

The Magic of Convolutions

  • feature engineering
    • creating new transformations of the input data in order to make it easier to the model
    • one of the most powerful tools machine learning practitioners have at their disposal
  • a feature is a transformation of the data that is designed to make it easier to the model

Convolution

  • applies a kernel across an image
    • multiplies each element of an \(NxN\) size kernel by each element of an \(NxN\) block of an image and adds the results together
  • kernel: a little matrix

A guide to convolution arithmetic for deep learning

  • provides many great diagrams showing how image kernels can be applied
# A convolutional kernel that finds top edges (i.e. dark on bottom, light on top)
top_edge = tensor([[-1,-1,-1],
                   [ 0, 0, 0],
                   [ 1, 1, 1]]).float()
path = untar_data(URLs.MNIST_SAMPLE)
path
Path('/home/innom-dt/.fastai/data/mnist_sample')
im3 = Image.open(path/'train'/'3'/'12.png')
show_image(im3);

show_image
<function fastai.torch_core.show_image(im, ax=None, figsize=None, title=None, ctx=None, cmap=None, norm=None, *, aspect=None, interpolation=None, alpha=None, vmin=None, vmax=None, origin=None, extent=None, interpolation_stage=None, filternorm=True, filterrad=4.0, resample=None, url=None, data=None, **kwargs)>
print_source(show_image)
@delegates(plt.Axes.imshow, keep=True, but=['shape', 'imlim'])
def show_image(im, ax=None, figsize=None, title=None, ctx=None, **kwargs):
    "Show a PIL or PyTorch image on `ax`."
    # Handle pytorch axis order
    if hasattrs(im, ('data','cpu','permute')):
        im = im.data.cpu()
        if im.shape[0]<5: im=im.permute(1,2,0)
    elif not isinstance(im,np.ndarray): im=array(im)
    # Handle 1-channel images
    if im.shape[-1]==1: im=im[...,0]

    ax = ifnone(ax,ctx)
    if figsize is None: figsize = (_fig_bounds(im.shape[0]), _fig_bounds(im.shape[1]))
    if ax is None: _,ax = plt.subplots(figsize=figsize)
    ax.imshow(im, **kwargs)
    if title is not None: ax.set_title(title)
    ax.axis('off')
    return ax
im3_t = tensor(im3)
im3_t[0:3,0:3] * top_edge
tensor([[-0., -0., -0.],
        [0., 0., 0.],
        [0., 0., 0.]])
(im3_t[0:3,0:3] * top_edge).sum()
tensor(0.)
df = pd.DataFrame(im3_t[:10,:20])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
  0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 12 99 91 142 155 246 182 155 155 155 155 131 52 0 0 0 0
6 0 0 0 138 254 254 254 254 254 254 254 254 254 254 254 252 210 122 33 0
7 0 0 0 220 254 254 254 235 189 189 189 189 150 189 205 254 254 254 75 0
8 0 0 0 35 74 35 35 25 0 0 0 0 0 0 13 224 254 254 153 0
9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 90 254 254 247 53 0 
df = pd.DataFrame(im3_t[4:7,6:9])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
  0 1 2
0 0 0 0
1 142 155 246
2 254 254 254 
(im3_t[4:7,6:9] * top_edge).sum()
tensor(762.)

Note: Returns a high number because the \(3x3\) pixel square represents a top edge.

df = pd.DataFrame(im3_t[7:10,17:20])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
  0 1 2
0 254 75 0
1 254 153 0
2 247 53 0 
(im3_t[7:10,17:20] * top_edge).sum()
tensor(-29.)

Note: Returns a low number because the \(3x3\) pixel square does not represent a top edge.

# Center coords of the 3x3 matrix will be (row,col)
def apply_kernel(row, col, kernel):
    return (im3_t[row-1:row+2,col-1:col+2] * kernel).sum()
apply_kernel(5,7,top_edge)
tensor(762.)

Mapping a Convolution Kernel

# Nested list comprehension to generate a list of coordinates
[[(i,j) for j in range(1,5)] for i in range(1,5)]
[[(1, 1), (1, 2), (1, 3), (1, 4)],
 [(2, 1), (2, 2), (2, 3), (2, 4)],
 [(3, 1), (3, 2), (3, 3), (3, 4)],
 [(4, 1), (4, 2), (4, 3), (4, 4)]]
rng = range(1,27)
# Map top edge kernel to the generated list of coordinates
top_edge3 = tensor([[apply_kernel(i,j,top_edge) for j in rng] for i in rng])

show_image(top_edge3);

Note: Top edges are black and bottom edges are white.

left_edge = tensor([[-1,1,0],
                    [-1,1,0],
                    [-1,1,0]]).float()

left_edge3 = tensor([[apply_kernel(i,j,left_edge) for j in rng] for i in rng])

show_image(left_edge3);

right_edge = tensor([[0,1,-1],
                     [0,1,-1],
                     [0,1,-1]]).float()

right_edge3 = tensor([[apply_kernel(i,j,right_edge) for j in rng] for i in rng])

show_image(right_edge3);

bottom_edge = tensor([[0,0,0],
                      [1,1,1],
                      [-1,-1,-1]]).float()

bottom_edge3 = tensor([[apply_kernel(i,j,bottom_edge) for j in rng] for i in rng])

show_image(bottom_edge3);

Convolutions in PyTorch

diag1_edge = tensor([[ 0,-1, 1],
                     [-1, 1, 0],
                     [ 1, 0, 0]]).float()
diag2_edge = tensor([[ 1,-1, 0],
                     [ 0, 1,-1],
                     [ 0, 0, 1]]).float()

edge_kernels = torch.stack([left_edge, right_edge, top_edge, bottom_edge, diag1_edge, diag2_edge])
edge_kernels.shape
torch.Size([6, 3, 3])
print_source(first)
def first(x, f=None, negate=False, **kwargs):
    "First element of `x`, optionally filtered by `f`, or None if missing"
    x = iter(x)
    if f: x = filter_ex(x, f=f, negate=negate, gen=True, **kwargs)
    return next(x, None)
mnist = DataBlock((ImageBlock(cls=PILImageBW), CategoryBlock), 
                  get_items=get_image_files, 
                  splitter=GrandparentSplitter(),
                  get_y=parent_label)

dls = mnist.dataloaders(path)
xb,yb = first(dls.valid)
xb.shape
torch.Size([64, 1, 28, 28])
# Move to CPU
xb,yb = to_cpu(xb),to_cpu(yb)
edge_kernels.shape,edge_kernels.unsqueeze(1).shape
(torch.Size([6, 3, 3]), torch.Size([6, 1, 3, 3]))
edge_kernels = edge_kernels.unsqueeze(1)
edge_kernels
tensor([[[[[-1.,  1.,  0.],
           [-1.,  1.,  0.],
           [-1.,  1.,  0.]]]],

    
    
            [[[[ 0.,  1., -1.],
               [ 0.,  1., -1.],
               [ 0.,  1., -1.]]]],


    
    
            [[[[-1., -1., -1.],
               [ 0.,  0.,  0.],
               [ 1.,  1.,  1.]]]],


    
    
            [[[[ 0.,  0.,  0.],
               [ 1.,  1.,  1.],
               [-1., -1., -1.]]]],


    
    
            [[[[ 0., -1.,  1.],
               [-1.,  1.,  0.],
               [ 1.,  0.,  0.]]]],


    
    
            [[[[ 1., -1.,  0.],
               [ 0.,  1., -1.],
               [ 0.,  0.,  1.]]]]])
batch_features = F.conv2d(xb, edge_kernels)
batch_features.shape
torch.Size([64, 6, 26, 26])
help(F.conv2d)
Help on built-in function conv2d:

conv2d(...)
    conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1) -> Tensor
    
    Applies a 2D convolution over an input image composed of several input
    planes.
    
    This operator supports :ref:`TensorFloat32<tf32_on_ampere>`.
    
    See :class:`~torch.nn.Conv2d` for details and output shape.
    
    Note:
        In some circumstances when given tensors on a CUDA device and using CuDNN, this operator may select a nondeterministic algorithm to increase performance. If this is undesirable, you can try to make the operation deterministic (potentially at a performance cost) by setting ``torch.backends.cudnn.deterministic = True``. See :doc:`/notes/randomness` for more information.



        
        Args:
            input: input tensor of shape :math:`(\text{minibatch} , \text{in\_channels} , iH , iW)`
            weight: filters of shape :math:`(\text{out\_channels} , \frac{\text{in\_channels}}{\text{groups}} , kH , kW)`
            bias: optional bias tensor of shape :math:`(\text{out\_channels})`. Default: ``None``
            stride: the stride of the convolving kernel. Can be a single number or a
              tuple `(sH, sW)`. Default: 1
            padding: implicit paddings on both sides of the input. Can be a string {'valid', 'same'},
              single number or a tuple `(padH, padW)`. Default: 0
              ``padding='valid'`` is the same as no padding. ``padding='same'`` pads
              the input so the output has the shape as the input. However, this mode
              doesn't support any stride values other than 1.
        

          .. warning::
              For ``padding='same'``, if the ``weight`` is even-length and
              ``dilation`` is odd in any dimension, a full :func:`pad` operation
              may be needed internally. Lowering performance.
    
        dilation: the spacing between kernel elements. Can be a single number or
          a tuple `(dH, dW)`. Default: 1
        groups: split input into groups, :math:`\text{in\_channels}` should be divisible by the
          number of groups. Default: 1
    
    Examples::
    
        >>> # With square kernels and equal stride
        >>> filters = torch.randn(8, 4, 3, 3)
        >>> inputs = torch.randn(1, 4, 5, 5)
        >>> F.conv2d(inputs, filters, padding=1)
for i in range(6):
    show_image(batch_features[0,i]);

Strides and Padding

  • appropriate padding ensures the output activation map is the same size as the original image
  • the necessary padding for an \(ksxks\) size kernel (where \(ks\) is an odd number) is ks//2
    • almost never use even size kernels

Stride

  • the amount of pixels the kernel moves across the image at each step
  • stride-1 convolutions (with appropriate padding) maintain the same image size
  • stride-2 convolutions are usefult for reducing the size of the output

Understanding the Convolution Equations

  • CNNs from different viewpoints
    • shows different visualizations for convolutions
  • A convolution can be represented as a special kind of matrix multiplication with two constraints
    1. some elements are always zero
    2. some elements are forced to have the same value
  • These constraints enforce a certain pattern of connectivity

Our First Convolutional Neural Network

  • the kernels for the convolutions are learned during training
    • the model will learn what features are useful for classification

Creating the CNN

simple_net = nn.Sequential(
    nn.Linear(28*28,30),
    nn.ReLU(),
    nn.Linear(30,1)
)
simple_net
Sequential(
  (0): Linear(in_features=784, out_features=30, bias=True)
  (1): ReLU()
  (2): Linear(in_features=30, out_features=1, bias=True)
)
broken_cnn = sequential(
    nn.Conv2d(1,30, kernel_size=3, padding=1),
    nn.ReLU(),
    nn.Conv2d(30,1, kernel_size=3, padding=1)
)
broken_cnn
Sequential(
  (0): Conv2d(1, 30, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (1): ReLU()
  (2): Conv2d(30, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)
broken_cnn(xb).shape
torch.Size([64, 1, 28, 28])

Note: We don’t need to specify the input dimensions for convolutional layers because they are automatically applied over each pixel

Note: We can use stride-2 convolutions to progressively decrease the size down to a single output for classification. * It is common to increase the number of features at the same time, to maintain the same amount of computation

def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res
simple_cnn = sequential(
    conv(1 ,4),            #14x14
    conv(4 ,8),            #7x7
    conv(8 ,16),           #4x4
    conv(16,32),           #2x2
    conv(32,2, act=False), #1x1
    # Flatten output to a single dimension
    Flatten(),
)
simple_cnn
Sequential(
  (0): Sequential(
    (0): Conv2d(1, 4, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
    (1): ReLU()
  )
  (1): Sequential(
    (0): Conv2d(4, 8, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
    (1): ReLU()
  )
  (2): Sequential(
    (0): Conv2d(8, 16, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
    (1): ReLU()
  )
  (3): Sequential(
    (0): Conv2d(16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
    (1): ReLU()
  )
  (4): Conv2d(32, 2, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  (5): Flatten(full=False)
)
simple_cnn(xb).shape
torch.Size([64, 2])
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)
learn.summary()
Sequential (Input shape: 64 x 1 x 28 x 28)
============================================================================
Layer (type)         Output Shape         Param #    Trainable 
============================================================================
                     64 x 4 x 14 x 14    
Conv2d                                    40         True      
ReLU                                                           
____________________________________________________________________________
                     64 x 8 x 7 x 7      
Conv2d                                    296        True      
ReLU                                                           
____________________________________________________________________________
                     64 x 16 x 4 x 4     
Conv2d                                    1168       True      
ReLU                                                           
____________________________________________________________________________
                     64 x 32 x 2 x 2     
Conv2d                                    4640       True      
ReLU                                                           
____________________________________________________________________________
                     64 x 2 x 1 x 1      
Conv2d                                    578        True      
____________________________________________________________________________
                     64 x 2              
Flatten                                                        
____________________________________________________________________________

Total params: 6,722
Total trainable params: 6,722
Total non-trainable params: 0

Optimizer used: <function Adam at 0x7f576a7d3430>
Loss function: <function cross_entropy at 0x7f57b69003a0>

Callbacks:
  - TrainEvalCallback
  - Recorder
  - ProgressCallback
learn.fit_one_cycle(2, 0.01)
epoch train_loss valid_loss accuracy time
0 0.063063 0.045171 0.987242 00:02
1 0.023533 0.026628 0.991168 00:01

Understanding Convolution Arithmetic

m = learn.model[0]
m
Sequential(
  (0): Conv2d(1, 4, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  (1): ReLU()
)

1 input channel, four output channels, and a 3x3 kernel

m[0].weight.shape
torch.Size([4, 1, 3, 3])
4*1*3*3
36
m[0].bias.shape
torch.Size([4])

Receptive Fields

  • the area of an image that is involved in the calculation of a layer

A Note About Twitter

  • Many of the top people in deep learning today are Twitter regulars
  • One of the main ways to stay up to date with interesting papers, software releases, and other deep learning news

Color Images

  • a color image is a rank-3 tensor
  • we don’t use the same convolutional kernel for all three color channels
  • kernel has a size of ch_in x 3 x 3 where ch_in is the number of input channels (e.g. 3 for RGB)
image2tensor
<function fastai.vision.core.image2tensor(img)>
print_source(image2tensor)
def image2tensor(img):
    "Transform image to byte tensor in `c*h*w` dim order."
    res = tensor(img)
    if res.dim()==2: res = res.unsqueeze(-1)
    return res.permute(2,0,1)

(<function fastai.vision.core.image2tensor(img)>, None)
im = image2tensor(Image.open(image_bear()))
im.shape
torch.Size([3, 1000, 846])
show_image(im);

_,axs = subplots(1,3)
for bear,ax,color in zip(im,axs,('Reds','Greens','Blues')):
    show_image(255-bear, ax=ax, cmap=color)

Improving Training Stability

path = untar_data(URLs.MNIST)
path
Path('/home/innom-dt/.fastai/data/mnist_png')
path.ls()
(#2) [Path('/home/innom-dt/.fastai/data/mnist_png/testing'),Path('/home/innom-dt/.fastai/data/mnist_png/training')]
Path(path/'training').ls()
(#10) [Path('/home/innom-dt/.fastai/data/mnist_png/training/2'),Path('/home/innom-dt/.fastai/data/mnist_png/training/4'),Path('/home/innom-dt/.fastai/data/mnist_png/training/1'),Path('/home/innom-dt/.fastai/data/mnist_png/training/6'),Path('/home/innom-dt/.fastai/data/mnist_png/training/5'),Path('/home/innom-dt/.fastai/data/mnist_png/training/9'),Path('/home/innom-dt/.fastai/data/mnist_png/training/3'),Path('/home/innom-dt/.fastai/data/mnist_png/training/0'),Path('/home/innom-dt/.fastai/data/mnist_png/training/8'),Path('/home/innom-dt/.fastai/data/mnist_png/training/7')]
def get_dls(bs=64):
    return DataBlock(
        blocks=(ImageBlock(cls=PILImageBW), CategoryBlock), 
        get_items=get_image_files, 
        splitter=GrandparentSplitter('training','testing'),
        get_y=parent_label,
        batch_tfms=Normalize()
    ).dataloaders(path, bs=bs)

dls = get_dls()
dls.show_batch(max_n=9, figsize=(4,4))

A Simple Baseline

  • more convolutional filters are likely required since there are more numbers to recognize
  • it is important to keep the number of filters smaller than the number of pixels in the kernel size
    • this forces the neural network to extract useful features
def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res
def simple_cnn():
    return sequential(
        # Increate starting kernel size and number of filters
        conv(1 ,8, ks=5),        #14x14
        conv(8 ,16),             #7x7
        conv(16,32),             #4x4
        conv(32,64),             #2x2
        conv(64,10, act=False),  #1x1
        Flatten(),
    )
from fastai.callback.hook import *
def fit(epochs=1):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit(epochs, 0.06)
    return learn

fastai ActivationStats

  • provides som handy utilities for plotting the activations during training
ActivationStats
fastai.callback.hook.ActivationStats
print_source(ActivationStats)
@delegates()
class ActivationStats(HookCallback):
    "Callback that record the mean and std of activations."
    order=-20
    def __init__(self, with_hist=False, **kwargs):
        super().__init__(**kwargs)
        self.with_hist = with_hist

    def before_fit(self):
        "Initialize stats."
        super().before_fit()
        self.stats = L()

    def hook(self, m, i, o):
        if isinstance(o, tuple): return self.hook_multi_ouput(o)
        o = o.float()
        res = {'mean': o.mean().item(), 'std': o.std().item(),
               'near_zero': (o<=0.05).long().sum().item()/o.numel()}
        if self.with_hist: res['hist'] = o.histc(40,0,10)
        return res

    def hook_multi_ouput(self,o_tuple):
        "For outputs of RNN which are [nested] tuples of tensors"
        res = []
        for o in self._flatten_tuple(o_tuple):
            if not(isinstance(o, Tensor)): continue
            res.append(self.hook(None, None, o))
        return res

    def _flatten_tuple(self, o_tuple):
        "Recursively flatten a [nested] tuple"
        res = []
        for it in o_tuple:
            if isinstance(it, tuple): res += self._flatten_tuple(it)
            else: res += [it]
        return tuple(res)

    def after_batch(self):
        "Take the stored results and puts it in `self.stats`"
        if self.training and (self.every is None or self.train_iter%self.every == 0):
            self.stats.append(self.hooks.stored)
        super().after_batch()

    def layer_stats(self, idx):
        lstats = self.stats.itemgot(idx)
        return L(lstats.itemgot(o) for o in ('mean','std','near_zero'))

    def hist(self, idx):
        res = self.stats.itemgot(idx).itemgot('hist')
        return torch.stack(tuple(res)).t().float().log1p()

    def color_dim(self, idx, figsize=(10,5), ax=None):
        "The 'colorful dimension' plot"
        res = self.hist(idx)
        if ax is None: ax = subplots(figsize=figsize)[1][0]
        ax.imshow(res, origin='lower')
        ax.axis('off')

    def plot_layer_stats(self, idx):
        _,axs = subplots(1, 3, figsize=(12,3))
        for o,ax,title in zip(self.layer_stats(idx),axs,('mean','std','% near zero')):
            ax.plot(o)
            ax.set_title(title)
learn = fit()
epoch train_loss valid_loss accuracy time
0 0.617736 0.533550 0.831100 00:08 
learn.activation_stats.plot_layer_stats(0)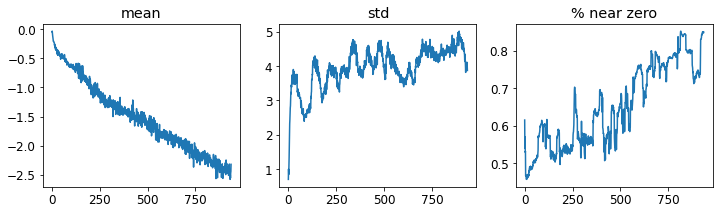

Note: Generally, the model should have a consisten (or at least smooth) mean and standard deviation of layer activations during training. * Activations near zero indicate we have computation in the model that is doing nothing at all * zeros in one layer generally carry over to the next layer, which will then create more zeros

# The penultimate layer
learn.activation_stats.plot_layer_stats(-2)

Note: The problems got wors toward the end of the network.

Increase Batch Size

  • a larger batch size can make training more stable
  • larger batches have more accurate gradients, since they are calculated from more data
  • larger batch sizes mean fewer batches per epoch, meaning fewer opportunities for your model to update weights
dls = get_dls(512)
learn = fit()
epoch train_loss valid_loss accuracy time
0 0.444612 0.259085 0.916200 00:05 
learn.activation_stats.plot_layer_stats(-2)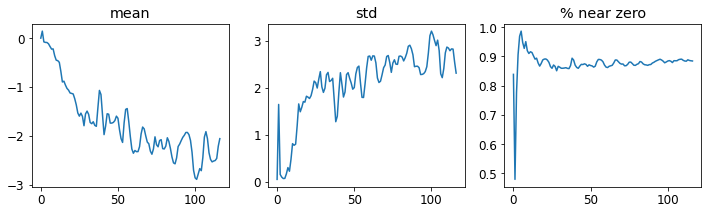

Note: Still a high number of activations near zero.

1cycle Training

  • it is dangerous to begin training with a high learning rate as the initial random weights are not well suited to the target task
  • don’t want to end with a high learning rate either
  • want to start with a smaller learning rate, then gradually increase it, then gradually decrease it again towards the end of training
  • Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates
    • designed a schedule for learning rate separated into two phases
      1. warmup: the learning rate grows from the minimum value to the maximum value
      2. annealing: the learning rate decreases back to the minimum value
  • 1cycle training allows us to use higher learning rates
    • allows us to train faster and reduces
    • results in less overfitting
      • we skip over sharp local minima in the loss landscape
      • we end up in a smoother, more generalizable part of the loss landscape
  • a model that generalizes well is one whose loss would not change much if you changed the input a little

Momentum

def fit(epochs=1, lr=0.06):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit_one_cycle(epochs, lr)
    return learn

fastai fit_one_cycle

  • uses cosine annealing instead of linear annealing
  • lr_max: the highest learning rate that will be used during training
    • single number for all layers
    • a list specifying learning rates for each layer group
    • a Python slice object containing learning rates for the first and last layer group
  • div: How much to divide lr_max by to get the starting learning rate
  • div_final: How much to divide lr_max by to get the ending learning rate
  • pct_start: What percentage of the batches to use for warmup
  • moms: a tuple (mom1,mom2,mom3)
    • mom1: the initial momentum
    • mom2: the minimum momentum
    • mom3: the final momentum
Learner.fit_one_cycle
<function fastai.callback.schedule.Learner.fit_one_cycle(self: fastai.learner.Learner, n_epoch, lr_max=None, div=25.0, div_final=100000.0, pct_start=0.25, wd=None, moms=None, cbs=None, reset_opt=False)>
print_source(Learner.fit_one_cycle)
@patch
def fit_one_cycle(self:Learner, n_epoch, lr_max=None, div=25., div_final=1e5, pct_start=0.25, wd=None,
                  moms=None, cbs=None, reset_opt=False):
    "Fit `self.model` for `n_epoch` using the 1cycle policy."
    if self.opt is None: self.create_opt()
    self.opt.set_hyper('lr', self.lr if lr_max is None else lr_max)
    lr_max = np.array([h['lr'] for h in self.opt.hypers])
    scheds = {'lr': combined_cos(pct_start, lr_max/div, lr_max, lr_max/div_final),
              'mom': combined_cos(pct_start, *(self.moms if moms is None else moms))}
    self.fit(n_epoch, cbs=ParamScheduler(scheds)+L(cbs), reset_opt=reset_opt, wd=wd)
print_source(ParamScheduler)
@docs
class ParamScheduler(Callback):
    "Schedule hyper-parameters according to `scheds`"
    order,run_valid = 60,False

    def __init__(self, scheds): self.scheds = scheds
    def before_fit(self): self.hps = {p:[] for p in self.scheds.keys()}
    def before_batch(self): self._update_val(self.pct_train)

    def _update_val(self, pct):
        for n,f in self.scheds.items(): self.opt.set_hyper(n, f(pct))

    def after_batch(self):
        for p in self.scheds.keys(): self.hps[p].append(self.opt.hypers[-1][p])

    def after_fit(self):
        if hasattr(self.learn, 'recorder') and hasattr(self, 'hps'): self.recorder.hps = self.hps

    _docs = {"before_fit": "Initialize container for hyper-parameters",
             "before_batch": "Set the proper hyper-parameters in the optimizer",
             "after_batch": "Record hyper-parameters of this batch",
             "after_fit": "Save the hyper-parameters in the recorder if there is one"}
learn = fit()
epoch train_loss valid_loss accuracy time
0 0.191914 0.067390 0.979200 00:05 
learn.recorder.plot_sched()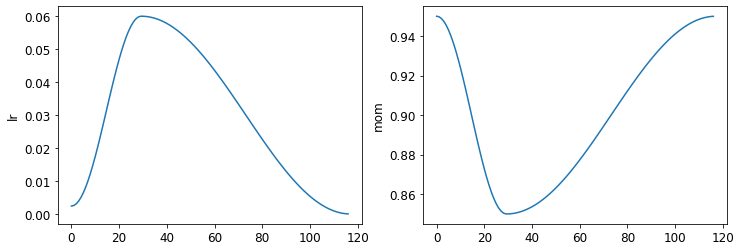

learn.recorder
Recorder
Recorder
fastai.learner.Recorder

fastai Recorder

  • Documentaion
  • records everything that happens during training including
    • losses
    • metrics
    • hyperparameters
      • learning rate
      • momentum
print_source(Recorder)
class Recorder(Callback):
    "Callback that registers statistics (lr, loss and metrics) during training"
    _stateattrs=('lrs','iters','losses','values')
    remove_on_fetch,order = True,50

    def __init__(self, add_time=True, train_metrics=False, valid_metrics=True, beta=0.98):
        store_attr('add_time,train_metrics,valid_metrics')
        self.loss,self.smooth_loss = AvgLoss(),AvgSmoothLoss(beta=beta)

    def before_fit(self):
        "Prepare state for training"
        self.lrs,self.iters,self.losses,self.values = [],[],[],[]
        names = self.metrics.attrgot('name')
        if self.train_metrics and self.valid_metrics:
            names = L('loss') + names
            names = names.map('train_{}') + names.map('valid_{}')
        elif self.valid_metrics: names = L('train_loss', 'valid_loss') + names
        else: names = L('train_loss') + names
        if self.add_time: names.append('time')
        self.metric_names = 'epoch'+names
        self.smooth_loss.reset()

    def after_batch(self):
        "Update all metrics and records lr and smooth loss in training"
        if len(self.yb) == 0: return
        mets = self._train_mets if self.training else self._valid_mets
        for met in mets: met.accumulate(self.learn)
        if not self.training: return
        self.lrs.append(self.opt.hypers[-1]['lr'])
        self.losses.append(self.smooth_loss.value)
        self.learn.smooth_loss = self.smooth_loss.value

    def before_epoch(self):
        "Set timer if `self.add_time=True`"
        self.cancel_train,self.cancel_valid = False,False
        if self.add_time: self.start_epoch = time.time()
        self.log = L(getattr(self, 'epoch', 0))

    def before_train   (self): self._train_mets[1:].map(Self.reset())
    def before_validate(self): self._valid_mets.map(Self.reset())
    def after_train   (self): self.log += self._train_mets.map(_maybe_item)
    def after_validate(self): self.log += self._valid_mets.map(_maybe_item)
    def after_cancel_train(self):    self.cancel_train = True
    def after_cancel_validate(self): self.cancel_valid = True

    def after_epoch(self):
        "Store and log the loss/metric values"
        self.learn.final_record = self.log[1:].copy()
        self.values.append(self.learn.final_record)
        if self.add_time: self.log.append(format_time(time.time() - self.start_epoch))
        self.logger(self.log)
        self.iters.append(self.smooth_loss.count)

    @property
    def _train_mets(self):
        if getattr(self, 'cancel_train', False): return L()
        return L(self.smooth_loss) + (self.metrics if self.train_metrics else L())

    @property
    def _valid_mets(self):
        if getattr(self, 'cancel_valid', False): return L()
        return (L(self.loss) + self.metrics if self.valid_metrics else L())

    def plot_loss(self, skip_start=5, with_valid=True):
        plt.plot(list(range(skip_start, len(self.losses))), self.losses[skip_start:], label='train')
        if with_valid:
            idx = (np.array(self.iters)<skip_start).sum()
            valid_col = self.metric_names.index('valid_loss') - 1
            plt.plot(self.iters[idx:], L(self.values[idx:]).itemgot(valid_col), label='valid')
            plt.legend()
Recorder.plot_sched
<function fastai.callback.schedule.Recorder.plot_sched(self: fastai.learner.Recorder, keys=None, figsize=None)>
print_source(Recorder.plot_sched)
@patch
def plot_sched(self:Recorder, keys=None, figsize=None):
    keys = self.hps.keys() if keys is None else L(keys)
    rows,cols = (len(keys)+1)//2, min(2, len(keys))
    figsize = figsize or (6*cols,4*rows)
    _, axs = plt.subplots(rows, cols, figsize=figsize)
    axs = axs.flatten() if len(keys) > 1 else L(axs)
    for p,ax in zip(keys, axs):
        ax.plot(self.hps[p])
        ax.set_ylabel(p)
learn.activation_stats.plot_layer_stats(-2)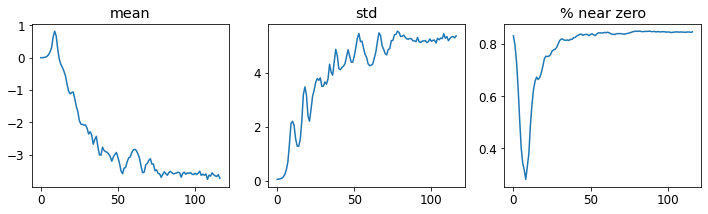

Note: The percentage of non-zero weight is better, but still high.

learn.activation_stats
ActivationStats
print_source(ActivationStats)
@delegates()
class ActivationStats(HookCallback):
    "Callback that record the mean and std of activations."
    order=-20
    def __init__(self, with_hist=False, **kwargs):
        super().__init__(**kwargs)
        self.with_hist = with_hist

    def before_fit(self):
        "Initialize stats."
        super().before_fit()
        self.stats = L()

    def hook(self, m, i, o):
        if isinstance(o, tuple): return self.hook_multi_ouput(o)
        o = o.float()
        res = {'mean': o.mean().item(), 'std': o.std().item(),
               'near_zero': (o<=0.05).long().sum().item()/o.numel()}
        if self.with_hist: res['hist'] = o.histc(40,0,10)
        return res

    def hook_multi_ouput(self,o_tuple):
        "For outputs of RNN which are [nested] tuples of tensors"
        res = []
        for o in self._flatten_tuple(o_tuple):
            if not(isinstance(o, Tensor)): continue
            res.append(self.hook(None, None, o))
        return res

    def _flatten_tuple(self, o_tuple):
        "Recursively flatten a [nested] tuple"
        res = []
        for it in o_tuple:
            if isinstance(it, tuple): res += self._flatten_tuple(it)
            else: res += [it]
        return tuple(res)

    def after_batch(self):
        "Take the stored results and puts it in `self.stats`"
        if self.training and (self.every is None or self.train_iter%self.every == 0):
            self.stats.append(self.hooks.stored)
        super().after_batch()

    def layer_stats(self, idx):
        lstats = self.stats.itemgot(idx)
        return L(lstats.itemgot(o) for o in ('mean','std','near_zero'))

    def hist(self, idx):
        res = self.stats.itemgot(idx).itemgot('hist')
        return torch.stack(tuple(res)).t().float().log1p()

    def color_dim(self, idx, figsize=(10,5), ax=None):
        "The 'colorful dimension' plot"
        res = self.hist(idx)
        if ax is None: ax = subplots(figsize=figsize)[1][0]
        ax.imshow(res, origin='lower')
        ax.axis('off')

    def plot_layer_stats(self, idx):
        _,axs = subplots(1, 3, figsize=(12,3))
        for o,ax,title in zip(self.layer_stats(idx),axs,('mean','std','% near zero')):
            ax.plot(o)
            ax.set_title(title)

fastai color_dim

  • Detailed Explanation
  • developed with fast.ai student Stefano Giomo
  • express with colors the mean and standard deviation of activations for each batch during training
  • vertical axis represents a group (bin) of activation values
  • each column in the horizontal axis is a batch
  • the colors represent how many activations for that batch have a value in that bin
# Set matplotlib color map
matplotlib.rcParams['image.cmap'] = 'viridis'
learn.activation_stats.color_dim(-2)

Note: This shows the classic picture of “bad training”: * Starts with nearly all activations at zero * The number of nonzero activations increases exponentially over the first few batches * Then it goes to far and collapses with most activations returning to zero or near-zero * This cycle repeats a few times before we see a spread of activations throughout the range * This can be addressed with batch normalization

Batch Normalization

  • take the average of the mean and standard deviations of the activations of a layer and use those to normalize that activations

    • this by itself can cause problems if the network wants some activations to be really high in order to make accurate predictions
      • resolved by adding two learnable parameters, gamma and beta
        • gamma*y + beta where y is a vector of normalize activations

  • Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

    • training deep neural networks is complicated by the fact that the distribution of each layer’s inputs changes during training, as parameters of the previous layers change
      • called covariate shift
      • slows down training by requiring lower learning rates and careful parameter initialization
      • resolved by normalizing layer inputs (each mini-batch)

  • batch normalization allows much higher learning rates and is less sensitive to parameter initialization

  • Different behavior during training and validation

    • training: use the mean and standard deviation of the batch to normalize the data
    • validation: use a running mean of the statistics calculated during training

  • models with batch normalization layers tend to generalize better

\(y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\)

nn.BatchNorm2d
torch.nn.modules.batchnorm.BatchNorm2d
print_source(nn.BatchNorm2d)
class BatchNorm2d(_BatchNorm):
    r"""Applies Batch Normalization over a 4D input (a mini-batch of 2D inputs
    with additional channel dimension) as described in the paper
    `Batch Normalization: Accelerating Deep Network Training by Reducing
    Internal Covariate Shift <https://arxiv.org/abs/1502.03167>`__ .

    .. math::

        y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta

    The mean and standard-deviation are calculated per-dimension over
    the mini-batches and :math:`\gamma` and :math:`\beta` are learnable parameter vectors
    of size `C` (where `C` is the input size). By default, the elements of :math:`\gamma` are set
    to 1 and the elements of :math:`\beta` are set to 0. The standard-deviation is calculated
    via the biased estimator, equivalent to `torch.var(input, unbiased=False)`.

    Also by default, during training this layer keeps running estimates of its
    computed mean and variance, which are then used for normalization during
    evaluation. The running estimates are kept with a default :attr:`momentum`
    of 0.1.

    If :attr:`track_running_stats` is set to ``False``, this layer then does not
    keep running estimates, and batch statistics are instead used during
    evaluation time as well.

    .. note::
        This :attr:`momentum` argument is different from one used in optimizer
        classes and the conventional notion of momentum. Mathematically, the
        update rule for running statistics here is
        :math:`\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momentum} \times x_t`,
        where :math:`\hat{x}` is the estimated statistic and :math:`x_t` is the
        new observed value.

    Because the Batch Normalization is done over the `C` dimension, computing statistics
    on `(N, H, W)` slices, it's common terminology to call this Spatial Batch Normalization.

    Args:
        num_features: :math:`C` from an expected input of size
            :math:`(N, C, H, W)`
        eps: a value added to the denominator for numerical stability.
            Default: 1e-5
        momentum: the value used for the running_mean and running_var
            computation. Can be set to ``None`` for cumulative moving average
            (i.e. simple average). Default: 0.1
        affine: a boolean value that when set to ``True``, this module has
            learnable affine parameters. Default: ``True``
        track_running_stats: a boolean value that when set to ``True``, this
            module tracks the running mean and variance, and when set to ``False``,
            this module does not track such statistics, and initializes statistics
            buffers :attr:`running_mean` and :attr:`running_var` as ``None``.
            When these buffers are ``None``, this module always uses batch statistics.
            in both training and eval modes. Default: ``True``

    Shape:
        - Input: :math:`(N, C, H, W)`
        - Output: :math:`(N, C, H, W)` (same shape as input)

    Examples::

        >>> # With Learnable Parameters
        >>> m = nn.BatchNorm2d(100)
        >>> # Without Learnable Parameters
        >>> m = nn.BatchNorm2d(100, affine=False)
        >>> input = torch.randn(20, 100, 35, 45)
        >>> output = m(input)
    """

    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError("expected 4D input (got {}D input)".format(input.dim()))
def conv(ni, nf, ks=3, act=True):
    layers = [nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)]
    layers.append(nn.BatchNorm2d(nf))
    if act: layers.append(nn.ReLU())
    return nn.Sequential(*layers)
learn = fit()
epoch train_loss valid_loss accuracy time
0 0.135761 0.058451 0.985700 00:06 
learn.activation_stats.color_dim(-4)

Note: Shows a smooth development of activations, with no crashes.

# Try training for longer and at a higher learning rate
learn = fit(5, lr=0.1)
epoch train_loss valid_loss accuracy time
0 0.185239 0.153986 0.951600 00:06
1 0.083529 0.110004 0.965800 00:06
2 0.052301 0.048957 0.984400 00:07
3 0.034640 0.032938 0.988600 00:06
4 0.017389 0.024644 0.991700 00:06 
learn = fit(5, lr=0.1)
epoch train_loss valid_loss accuracy time
0 0.187077 0.099310 0.969900 00:06
1 0.077691 0.089945 0.972400 00:06
2 0.050960 0.061807 0.980500 00:06
3 0.033020 0.030316 0.989600 00:06
4 0.017050 0.023186 0.992000 00:06

References

Previous: Notes on fastai Book Ch. 12

Next: Notes on fastai Book Ch. 14

About Me:

I’m Christian Mills, a deep learning consultant specializing in practical AI implementations. I help clients leverage cutting-edge AI technologies to solve real-world problems.

Interested in working together? Fill out my Quick AI Project Assessment form or learn more about me.